Given that \(y = \sin x\) and there is a transformation of a dilation of 2 vertical and dilation of \(\dfrac{1}{2}\) horizontal then the new function is ?

Given that  \(y = \cos x\) and there is a transformation of a dilation of \(\dfrac{1}{2}\) horizontal and a translation \(\dfrac{\pi }{4}\) units left, the new function is ? 

For the domain \(0 \le x \le 2\pi \) the solutions to \(2\cos (x - \dfrac{\pi }{3}) = 1\) are ?

For the domain \( - \pi \le x \le \pi \) the solutions to \(\sqrt 3 \tan 2x = 1\) are

\(f(x) = m\sin nx\) has a period of \(\pi\). If \(f'(x) = n\cos nx\),

(i) Find \(m\) and \(n\).

(ii) Sketch the function in the domain \(0 \leq x \leq m\pi\)

(i) Sketch the graph of \(y = 3\sin x\) for \(0 \leq x \leq 2\pi\). On the same set of axes, sketch the graph of \(y = 1-2\sin x\) for \(0 \leq x \leq 2\pi\).

(ii) The graphs intersect twice in the domain \(0 \leq x \leq \pi\). Find, in terms of radians, correct to one decimal place, the \(x\)-coordinates of these points of intersection.

Sketch the graph of \(y = -3\sin 2x\) for \(-\pi \leq x \leq \pi\).

(i) What is the maximum value of the function?

(ii) What is the period of the function?

The amplitude and period of \(y = - 3\sin 2x\) are: 

For the domain \(0 \le x \le 2\pi \) the solution to \(2\sin (x + \dfrac{\pi }{4}) = 1\) are :

For the curve \(y = \sin x + \cos x\) in the domain \(0 \le x \le 2\pi \), find the maximum turning point. 

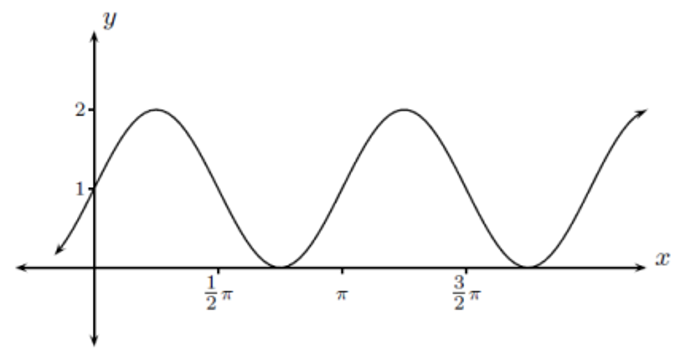
The equation of the graph sketched above could be: