Homepage

Course Index

Build a Quiz

Subscriptions

Courses

NSW Y11 Maths Standard NSW Y11 Maths Advanced NSW Y11 Maths Extension 1

Topics

Functions Polynomials Inverse Trig Functions and Identities Rates of Change Permutations and Combinations

NSW Y11 Maths - Extension 1 Polynomials Polynomial Graphs

Resources for Polynomial Graphs

  • Questions

    18

    With Worked Solution
    Click Here
  • Video Tutorials

    2


    Click Here
  • HSC Questions

    4

    With Worked Solution
    Click Here

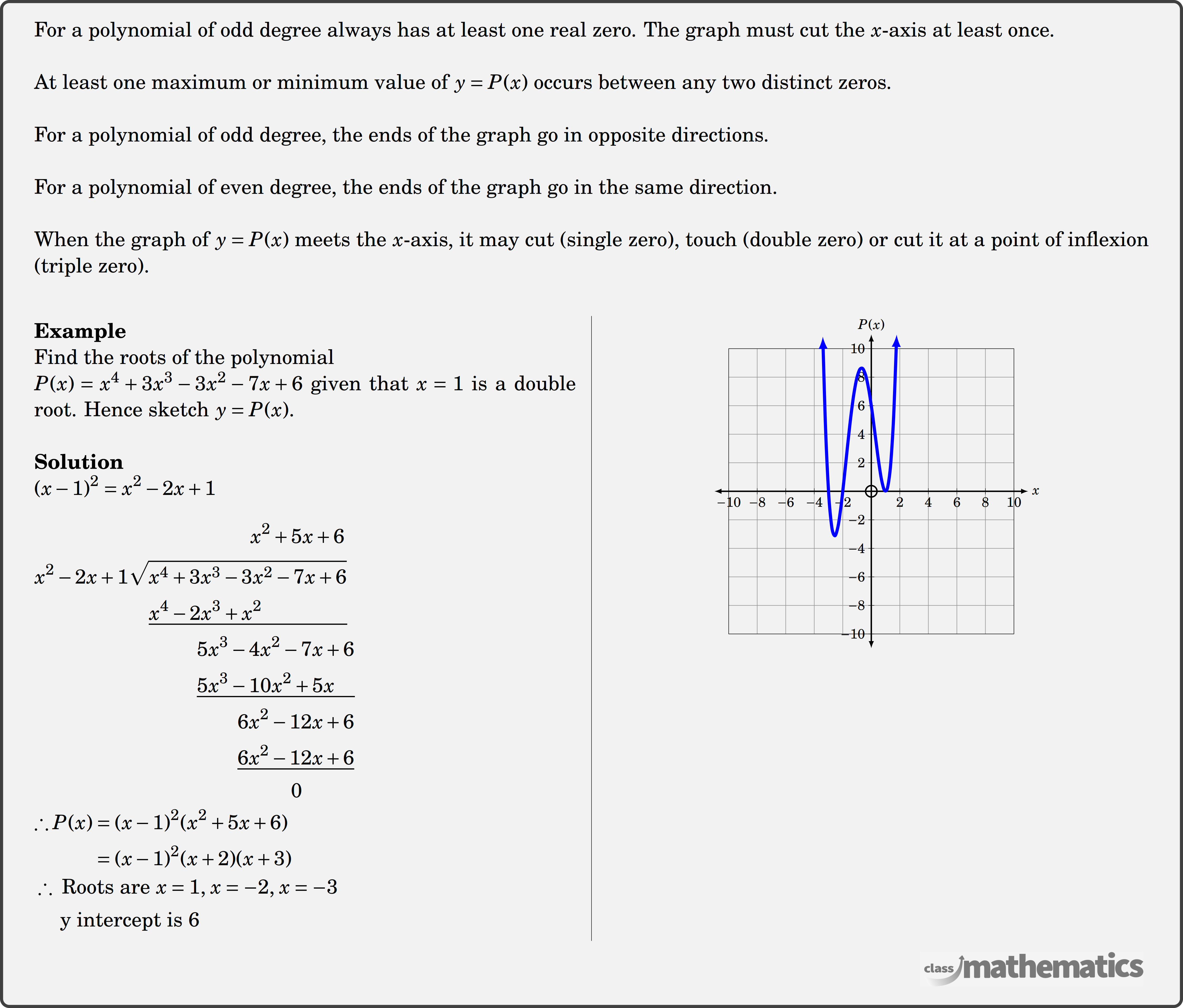
Polynomial Graphs Theory

NSW Syllabus Reference

NSW Syllabus Reference: ME-F2.2: Sums and products of roots of polynomials. This will require student to 

  • solve problems using the relationships between the roots and coefficients of quadratic, cubic and quartic equations
  • determine the multiplicity of a root of a polynomial equation
  • graph a variety of polynomials and investigate the link between the root of a polynomial equation and the zero on the graph of the related polynomial function

Ref: https://educationstandards.nsw.edu.au/

Create account

Access content straight away with a two week free trial

I am..

Please enter your details

I agree with your terms of service




Videos

Videos relating to Polynomial Graphs.

  • Polynomial Graphs - Video- Polynomial Graphs

    You must be logged in to access this resource

  • Polynomial Graphs - Video - Graphing Polynomial Functions Using End Behavior, Zeros, and Multiplicities

    You must be logged in to access this resource

Plans & Pricing

With all subscriptions, you will receive the below benefits and unlock all answers and fully worked solutions.

  • Teachers Tutors
    Features
    Free
    Pro
    All Content
    All courses, all topics
     
    Questions
     
    Answers
     
    Worked Solutions
    System
    Your own personal portal
     
    Quizbuilder
     
    Class Results
     
    Student Results
    Exam Revision
    Revision by Topic
     
    Practise Exams
     
    Answers
     
    Worked Solutions
  • Awesome Students
    Features
    Free
    Pro
    Content
    Any course, any topic
     
    Questions
     
    Answers
     
    Worked Solutions
    System
    Your own personal portal
     
    Basic Results
     
    Analytics
     
    Study Recommendations
    Exam Revision
    Revision by Topic
     
    Practise Exams
     
    Answers
     
    Worked Solutions

Theory

For a polynomial of odd degree always has at least one real zero. The graph must cut the \(x\)-axis at least once.

At least one maximum or minimum value of \(y = P(x)\) occurs between any two distinct zeros.

For a polynomial of odd degree, the ends of the graph go in opposite directions.

For a polynomial of even degree, the ends of the graph go in the same direction.

When the graph of \(y = P(x)\) meets the \(x\)-axis, it may cut (single zero), touch (double zero) or cut it at a point of inflexion (triple zero).