Homepage

Course Index

Build a Quiz

Subscriptions

Courses

NSW Y11 Maths Standard NSW Y11 Maths Advanced NSW Y11 Maths Extension 1

Topics

Functions Polynomials Inverse Trig Functions and Identities Rates of Change Permutations and Combinations

NSW Y11 Maths - Extension 1 Functions Absolute Value Functions

Resources for Absolute Value Functions

  • Questions

    13

    With Worked Solution
    Click Here
  • Video Tutorials

    1


    Click Here
  • HSC Questions

    3

    With Worked Solution
    Click Here

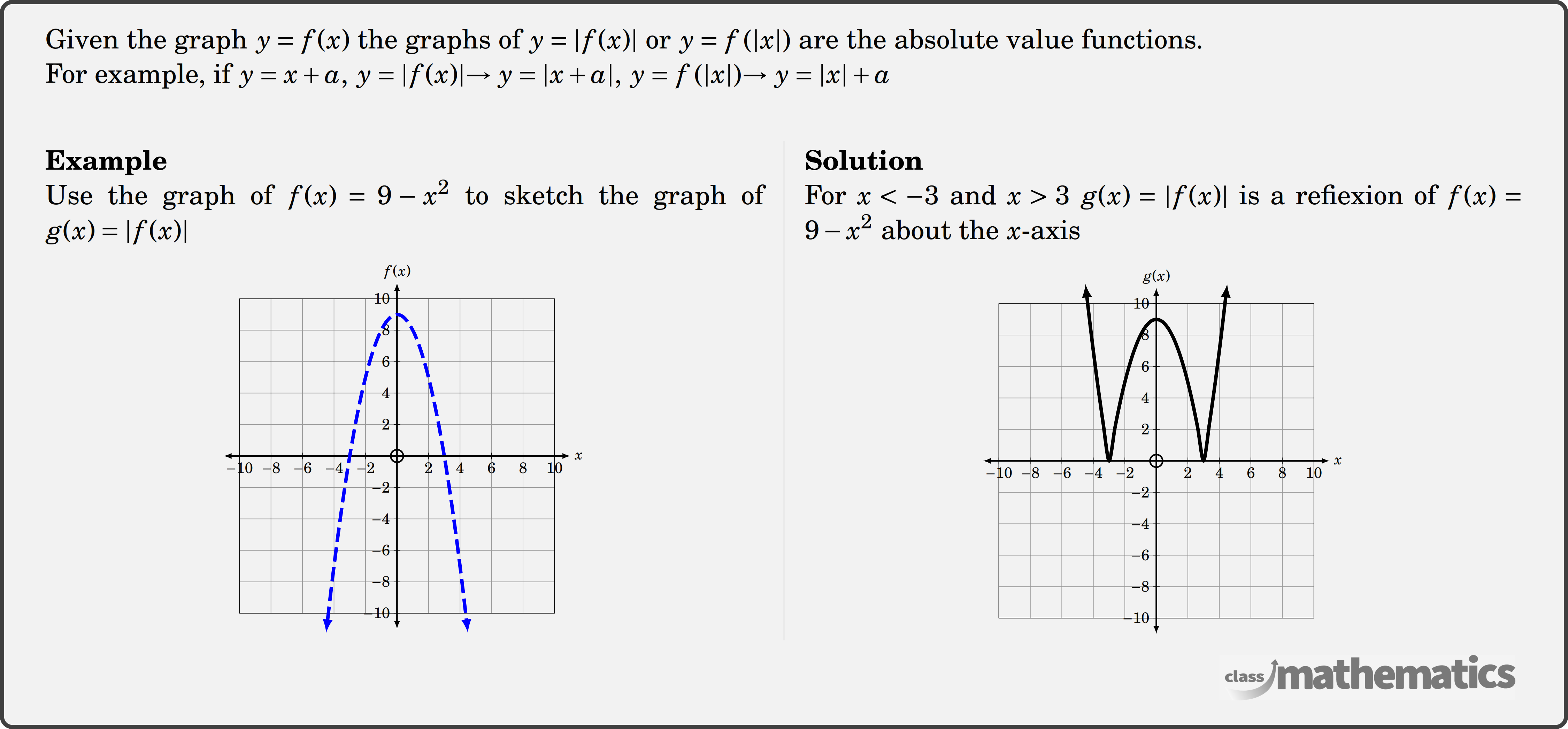
Absolute Value Functions Theory

Create account

I am..

Please enter your details

I agree with your terms of service




Videos

Videos relating to Absolute Value Functions .

  • Absolute Value Functions - Video - Graphing Absolute Value Functions

    You must be logged in to access this resource

Plans & Pricing

With all subscriptions, you will receive the below benefits and unlock all answers and fully worked solutions.

  • Teachers Tutors
    Features
    Free
    Pro
    All Content
    All courses, all topics
     
    Questions
     
    Answers
     
    Worked Solutions
    System
    Your own personal portal
     
    Quizbuilder
     
    Class Results
     
    Student Results
    Exam Revision
    Revision by Topic
     
    Practise Exams
     
    Answers
     
    Worked Solutions
  • Awesome Students
    Features
    Free
    Pro
    Content
    Any course, any topic
     
    Questions
     
    Answers
     
    Worked Solutions
    System
    Your own personal portal
     
    Basic Results
     
    Analytics
     
    Study Recommendations
    Exam Revision
    Revision by Topic
     
    Practise Exams
     
    Answers
     
    Worked Solutions

Theory

Given the graph \(y = f(x)\) the graphs of \(y = \left| {f(x)} \right|\) or \(y = f\left( {\left| x \right|} \right)\) are the absolute value functions.

For example, if \(y = x + a\), \(y = \left| {f(x)} \right|\)\( \to y = \left| {x + a} \right|\), \(y = f\left( {\left| x \right|} \right)\)\( \to y = \left| x \right| + a\)

Syllabus Reference

NSW Syllabus Reference: ME-F1.1: Graphical relationships. This will require student to 

  • examine the relationship between the graph of \(y=f(x)\) and the graph of \(y=\dfrac{1}{f(x)}\) and hence sketch the graphs (ACMSM099)
  • examine the relationship between the graph of \(y=f(x)\) and the graphs of \(y^2=f(x)\) and \(y=\sqrt{f(x)}\) and hence sketch the graphs
  • examine the relationship between the graph of \(y=f(x)\) and the graphs of \(y=|f(x)|\) and \(y=f(x)+g(x)\) and hence sketch the graphs (ACMSM099)
  • examine the relationship between the graphs of \(y=f(x)\) and \(y=g(x)\) and the graphs of \(y=f(x)+g(x)\) and \(y=f(x)g(x)\) and hence sketch the graphs
  • apply knowledge of graphical relationships to solve problems in practical and abstract contexts

Ref: https://educationstandards.nsw.edu.au/