NSW Y9 Maths Advanced Equations Quadratic Equations

With all subscriptions, you will receive the below benefits and unlock all answers and fully worked solutions.

An equation in which the highest power of the variable is 2 is called a quadratic equation, for example, \(y = 2{x^2} + 5\).

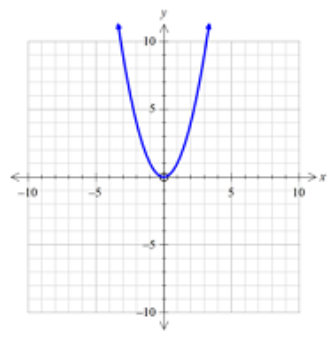
The graph of \(y = {x^2}\) is of parabola's shape and is concave up with turning point or vertex as \((0,0)\).

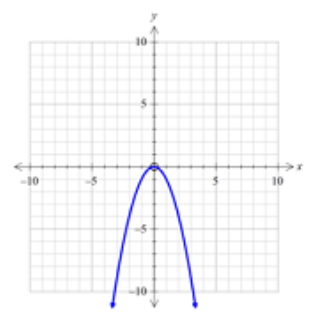
The graph of \(y = -{x^2}\) is of parabola's shape and is concave down with turning point or vertex as \((0,0)\).

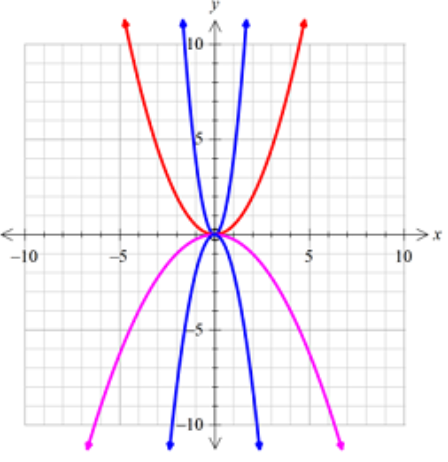
The graph of \(y = a{x^2}\) where \(a\) is a constant (number), the size of \(a\) affects whether the parabola is 'wide' or 'narrow'. For example,

\(y = \frac{{{x^2}}}{2},y = - 4{x^2}\). 

The graph of \(y = a{x^2}+c\) where \(a\) and \(c\) are constants, the effect of \(c\) is to move the parabola up or down from the origin.

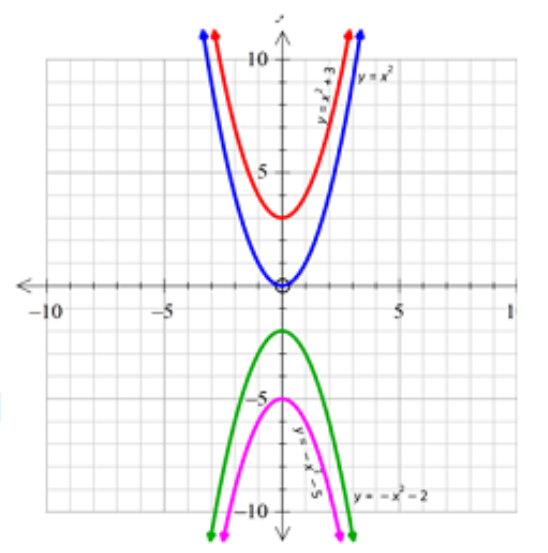
Example 1

a. Graph \(y={x^2},y={x^2}+3,y=-{x^2}-2 and y=-{x^2}-5\) on the same set of axes.

b. Compare each parabola with the parabola \(y={x^2}\)

\(y={x^2}+3\) is \(y={x^2}\) shifted up \(3 units\)

\(y=-{x^2}-2\) is \(y={x^2}\) turned upside down and shifted down \(2 units\)

\(y=-{x^2}-5\) is \(y={x^2}\) turned upside down and shifted down \(5 units\)

c. What is the vertex of each parabola and is each parabola concave up or concave down?

\(y={x^2}\) has vertex \((0,0)\) and is concave up.

\(y={x^2}+3\) has vertex \((0,3)\) and is concave up.

\(y=-{x^2}-2\) has vertex \((0,-2)\) and is concave down.

\(y=-{x^2}-5\) has vertex \((0,-5)\) and is concave down.